
 |
| M mxn: |
M: Nombre de la matriz.
m: Numero de Filas.
n: Numero de columnas
n: Numero de columnas
TIPOS DE MATRICES
Los tipos de matrices se determinan por las dimensiones que las mismas contengan. Las dimensiones están determinadas por el numero de filas y de columnas que contengan:
- MATRIZ DIAGONAL PRINCIPAL: Consta de los elementos que conforman la diagonal que esta de izquierda a derecha y la diagonal secundaria sera lo contrario, y no puede contener 0 (cero) entre sus elementos. solo se identifican las diagonales, en las matrices cuadradas.
- MATRIZ TRIANGULAR: Ésta debe tener dos condiciones, la primera debe ser cuadrada y ademas los elementos que quedan por debajo de la diagonal principal son nulos, o bien los elementos que están sobre la diagonal. Pueden ser superior o inferior.
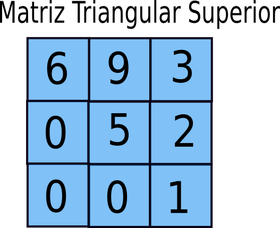  |
| INFERIOR SUPERIOR |
- MATRIZ DIAGONAL: Son matrices cuadrada en la que todos los elementos fuera de la diagonal principal son 0 (cero).
- MATRIZ UNIDAD O IDENTIDAD: Es una matriz diagonal, cuyos elementos de la diagonal principal son todos 1 (uno).
- MATRIZ CERO: Es aquella matriz donde todos los elementos deben ser cero.
- MATRIZ COLUMNA: Es cualquiera con una sola columna, es decir, sus dimensiones siempre serán m x 1.
- MATRIZ FILA: Es cualquiera con una unica fila y sus dimensiones siempre serán 1 x n.
- MATRIZ OPUESTA: A todos los elementos de la matriz original, tienen que cambiarle ls signos por el opuesto.
- MATRIZ CUADRADA: Está representada el mismo número de filas que de columna, e sdecir, sus dimensiones siempre van a ser m = n.
- MATRIZ TRANSPUESTA: Es donde se intercambian el numero de filas por el numero de columnas.
SUMA DE MATRICES
Para sumar matrices, todas deben contener las mismas dimensiones y solo se pueden sumar los elementos que tengan las mismas posiciones.
"SUMA EL PRIMER ELEMENTO DE LA PRIMERA MATRIZ
CON EL PRIMER ELEMENTO DE LA SEGUNDA MATRIZ.
EL SEGUNDO CON EL SEGUNDO. TERCERO CON EL TERCERO. ASÍ SUCESIVAMENTE CON CADA UNO QUE SE ENCUENTREN EN EL MISMO LUGAR"
RESTA DE MATRICES
Se debe multiplicar por menos (-) la segunda matriz o la que representa el signo negativo adelante de ella
Para sumar matrices, todas deben contener las mismas dimensiones y solo se pueden sumar los elementos que tengan las mismas posiciones.
CON EL PRIMER ELEMENTO DE LA SEGUNDA MATRIZ.
EL SEGUNDO CON EL SEGUNDO. TERCERO CON EL TERCERO. ASÍ SUCESIVAMENTE CON CADA UNO QUE SE ENCUENTREN EN EL MISMO LUGAR"
RESTA DE MATRICES
"NO ES COMPLICADO MULTIPLICAR POR MENOS LA SEGUNDA MATRIZ O LA DEL SIGNO NEGATIVO, SOLO DEBES RECORDAR LA REGLA DE LOS SIGNOS (iguales: + diferentes: -). EL SIGNO NEGATIVO LO MULTIPLICAS POR CADA SIGNO DE CADA ELEMENTO.

MULTIPLICACIÓN DE
UN ESCALAR
PARA UNA MATRIZ
Se multiplica cada elemento por el escalar, incluyendo los signos.
"Un escalar son números reales, constantes o complejos que sirven para describir un fenómeno físico (o de otro tipo) con magnitud, pero sin la característica vectorial de dirección".
**MULTIPLICA EL ESCALAR CON SU SIGNO POR CADA ELEMENTO**
MULTIPLICACIÓN DE MATRICES
La multiplicación de dos matrices se da solo en el caso de que el numero de columnas de la primera matriz, sea igual al numero de filas de la segunda matriz. En el caso contrario, la multiplicación de matrices no es tan definida.
"LA PRIMERA FILA DE LA PRIMERA MATRIZ LA MULTIPLICAS POR CADA COLUMNA DE LA OTRA MATRIZ, AL IGUAL QUE LA SEGUNDA FILA, TERCERA, Y CADA UNA DE ELLAS"
¡Practica y Aprende!
¿Quieres ser un experto en matrices? ¿Deseas aprender mucho mas? ¿No tienes un lugar fácil, rápido y cómodo para realizar tus operaciones?
 Prueba Tú Ingenio |
